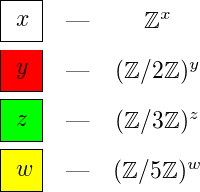-homology of the T(6,5)-torus knot:

q \ t	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19
-78																				1
-76																			1
-74																		1	1
-72																	2	1	1 1 1
-70															1		2 1	2 1
-68													1		2	1	1 3	2
-66													2		1 3	4	1	1 1
-64											1		2 1	4	2	3 1	1
-62											1	2	2	5 1	1 1	1 1	1
-60									1	1	1	5	1	1 1 3	2
-58									1	4		3 2	3	1	1
-56								2	1	4 1	1	1 2	3
-54						1		3	1	1 2	3		1
-52						2		1 1	3	1	1
-50				1		1 1	2		3
-48				1	1	1	2		1
-46				1	2		1
-44			1		1
-42	1		1
-40	1
-38	1

Computed in six minutes on an AMD Opteron, 2.2GHz, using 80MB of RAM.
Diagram drawn with the KnotTheory` package for Mathematica.

For details, see my paper -foam homology calculations: arxiv.org/abs/1212.2553.

Download

foamho-1.1.tar.gz containing the source code and installation instructions in the README file. To compile, you will need at least the MPIR-library, which is used for rational and integral arbitrary precision arithmetic. Optionally, the PARI-library is used to obtain smith normal forms (not necessary if you only want to compute rational homology), and the PROCPS-library to display memory consumption (on Linux only).

foamho.exe, a windows executable compiled using minGW running on Windows XP. No additional libraries necessary, but it is not guaranteed to work on your system.

foamho, a linux executable. No additional libraries are necessary, but it is not guaranteed to work on your system.

Old version (1.0): foamho-1.0.tar.gz, foamho.exe, foamho.

Some results

• Unreduced sl3-homology of knots with up to 12 crossings
• Reduced sl3-homology of knots with up to 12 crossings
• Unreduced sl3-homology of links with up to 11 crossings

Let us list all knots of twelve or less crossings for which the - and -concordance invariants differ (click on the knot to see his diagram on the Knot Atlas or on KnotInfo). In our normalisation, both invariants have a value of 2 for the right-handed trefoil knot.